Elastic Maps and Word Embeddings

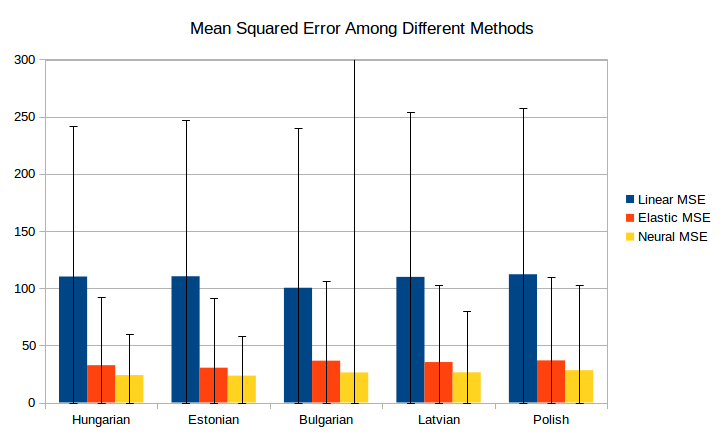
Recently for a class in Machine Translation I did another sort of manifold learning type task.

The premise of the problem was this: Using Google's Word2Vec you can take a sentence and learn "word embeddings", or N-dimensional euclidean vectors, that are supposed to encode the meaning of each word. Similar words should be embedded in similar places. What if you do this for two translations of a text? Can you use the word embeddings in one language to predict the embeddings in another?

The answer is a solid sorta.

First for why word embeddings are important at all.

Usually when you have a sentence, you encode it as a sequence of really high dimensional one-hot vectors. In other words you'll have a V dimensional vector - where V is the total number of unique words, i.e. in the millions for any substantial text - and for each vector it will be all zeroes and then just one 1 in the spot corresponding to whichever word it is. There's a few problems with this, first off the dimensionality is probably way too high -- which is something we can take advantage of (this is very similar to the idea of Self Organizing Maps which I've covered before). And second off, the dimensionality is way too high -- to do a Neural Model we would have to have an insane amount of nodes to be able to reduce that to a reasonable point. And third off, those vectors tell us nothing. The distance between any two words is identical -- there's absolutely no semantic content loaded in those word embeddings.

So what we do is we run it through a fancy neural network black box, and then figure out a reduced dimensional representation of the word that hopefully encodes some of the relations between words.

Now that we have word embeddings though, can we do anything fancy with them? Ideally across languages words should embed in the same spots if they have the same idea, unfortunately they don't with our current methods -- but we sort of hope that we can use the spatial relations in one language to be able to help translate in another as a sort of language model.

There has been some work on finding maps between parallel word embeddings in the past, but all of the methods my partners and I found were very linear -- the primary one being to find the best fitting rotation between the data. That didn't sit well with me -- linearity is a really big assumption to make, and the way word embeddings are generated there's no guarantee of a linear relation.

So with my love of manifolds and my partner's begrudging allowance, we decided for our Machine Translation final project to take on this task, and try and show that a very nonlinear transformation would work better than the current linear method.

​And....

It did! By a lot. (That error bar for Bulgarian on the neural model is right by the way, and I'll touch on that later)

What did we do though? Well if you remember me mentioning Self Organizing Maps earlier, we tried something very similar. What we modified was an algorithm called an Elastic Map which is a very similar idea. Instead of just uniformly pulling on the closest representation node as we did for the SOM, we create a "Springy Mesh" over the space, and pull on that mesh towards our training data. We had to modify the algorithm however, as like a SOM, Elastic Maps find a manifold over the data, and we don't want a manifold, we want a linear transformation.

So we modified the Elastic Map to approximate the specific transformation we wanted, as well as encode the information we needed to make a transformation. The precise details you can read about in our writeup (which will be posted here) or look through in our code (here), but the jist of it is we defined three forces on our springy mesh: A deformation force that pulls the nodes we want mapped to specific spots towards those spots, a "continuity" force that pulls nodes near one another near one another, and a "linearity" force that has "ribs" of triplets of nodes and tries to pull the middle node to the spot between the two outer nodes (resisting the map getting way too twisted). Once we have those three forces we can compute gradient descent to optimize our map.

And the map performed really well! You can see in the above graph that the average error is almost consistently less than a quarter of the linear method, and by the error bars (which represent one standard deviation of MSE) even at the worst case in one standard deviation it still is outperforming the average case for the linear method.

We also ran a neural network, because you can never talk about maps without doing neural networks, and what we found is that our method is good (although lacking in tuning, as time was running short on our final project) on average the neural network beats it, however something interesting happened. In the above ran model, on Bulgarian the neural model had a standard deviation of over 400. On just about each neural model ran, there was some dataset that the model on average preformed well, but had a large tail of extreme outliers, whereas the elastic map performed very consistently.

So while there's definitely room for improvement with the elastic map model, this first foray into implementing it I think definitely showed that it is a method worth looking into.